

|
On the 21st of August (2007) our colleague Jan Verhoeven retired. Jan spent his whole professional career as a semiconductor IC technologist in various Philips research clean rooms. During the 35 years that he was involved in silicon processing, Jan was part of a number of important innovations such as: LOCOS, RESURF etc. No doubt his vast experience will be sadly missed, especially since Jan was one of the last of a generation who could almost entirely overlook the total area of silicon processing.
When Jan joined Philips, processing was still done on 1 inch silicon wafers. Over the years the wafer diameter increased, and the largest wafer size that Jan worked on was 200 mm diameter. It is often said that size does not matter. True as this may be in general, it does not hold when it comes down to making farewell presents. In our line of work, 150 mm and 200 mm silicon wafers often form the base for a memento that is supposed to remind it's recipient on his or hers career. A clock using as silicon wafer as dial is often a favorite present, also in this case.
Over the years, Jan has witnessed many changes in the way Research operates, and not all changes represented progress! Since Jan was always been keenly aware of this, we decided to make him a clock that appropriately runs backwards. On more than one occasion Jan has indicated how much he liked the colored LEDs and poly-LED displays which sometimes are used in the jubilee and farewell presents that are being made. Since Jan is a special person, we decided to include a special color LED effect. The Roman numbers in the dial of the clock have been removed by laser cutting, and three color LEDs were placed behind them. A light effect consisting of a random sequence of colors that slowly fade into each other is generated by a specially designed PIC microcontroller circuit.
As Sherlock Holmes would say: "The design and programming of the circuit was not completely without interest", and certainly it was interesting enough to spend a web page on it. The stand alone circuit described here is based on a small PIC processor. Alternatively the subroutine which generates the color effect may run in the background of many other PIC programs so that it can be used to add light effects to other PIC applications.
| to top of page | back to homepage |
The circuit diagram of the light ornament is very simple (Fig. 1). The heart
of the circuit is an eight pin 12F675A micro controller. The 12F675A is one
of my favorite processors in the MICROCHIP PIC product line. It houses 1k byte
of flash, 64 bytes of RAM, 128 bytes of EEPROM and a wealth of peripherals,
all in a small 8 pin DIL package.
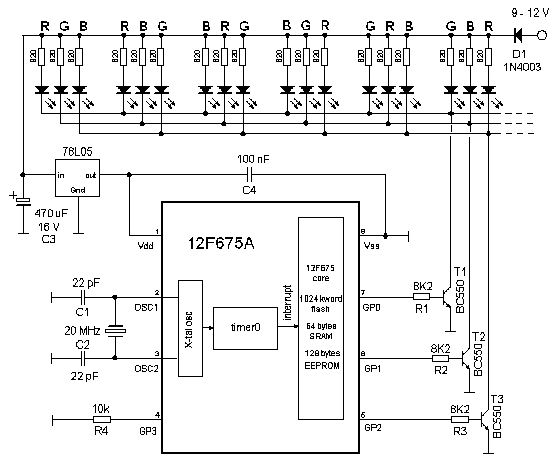
Figure 1. Circuit diagram of the color LED ornament.
Click on the picture
to open a window with the circuit diagram in pdf format.
The 12F675A has several clock modes. At the beginning of the project it was
not clear how much CPU power would be needed to drive the LEDs. Therefore I
decided to run the processor at it's maximum speed using a 20 MHz external
X-tal. The 12F675A however, also has the possibility to run an internal 4 MHz
oscillator. This saves an X-tal, two capacitors, power and adds another
two I/O pins. As it turned out, the program was reasonable efficient so
that it was also possible to run it on the 4 MHz internal clock, thereby
consuming about 50% of the CPU capacity. The 4 MHz version is discussed at the
end of this page.

Figure 2. Front and back side of the PCB
I/O's GPIO0, GPIO1 and GPIO2 are configured as outputs and drive the LEDs.
Pulse width modulation (see section on Color Generation)
is used to control the intensity of the LEDs. Figures 1 and 3 shows how by cyclic
rotation of the connections to each of the LEDs, six different colors are
obtained. The colors are however not completely uncorrelated; the relative
distance of each color to the white centre of the color triangle is the same
for each of the six LEDs. This implies for example that they all show a primary
color, or all show a more whitish color at the same time. The set of six
LEDs in Fig. 3 is repeated once to yield a total of twelve LEDs.
The 12F675A is capable of driving only one or two LEDs. In order to drive
twelve LEDs, separate discrete driver transistors were added. A simple
"small signal" type BC550 (BVCEO=45 V, Ft=300 MHz) turned out to be sufficient
to drive the LEDs with pulse widths at least down to 100 µs.

Figure 3. Final assembly with the twelve LEDs which are to be mounted behind the numbers in the dial of the clock. The detail shows the Red, Yellow and Blue LED dies in the package.
The circuit is powered by a low-cost wal-mart adapter of 9-12 V. The LEDs are powered directly from the unregulated supply, while the processor is powered via a low-power 78L05 regulator. During normal operation the circuit draws 10-25 mA per LED at 12V.
| to top of page | back to homepage |
When I promised to make this circuit, I estimated that the software wouldn’t present any particular difficulties: the LEDs were to be driven by pulse width modulation, and by slowly varying the on-off duty cycle of the LEDs, the resultant color would slowly move its way through the color triangle.
The program turned out to be a little bit trickier than I expected. Lets consider an example to illustrate the difficulty that was encountered. Suppose that we want to change the color from color_A to color_B in say 4 seconds. Lets furthermore assume that the transition is done in 100 discrete small steps, each with a duration of 0.04 s. Lets finally assume that color_A consists of (R=5%, Y=45%, B=70%) and color_B (R=95%, Y=50%, B=70%). The increment per color is given by (%A-%B)/100 or (dR=0.9, dY=0.05, dB=0) in %/step. This is all pretty straight forward, but it does require some double byte arithmetic like subtractions and divisions what you don't want to do if you can possibly avoid it.
In a next idea much of the arithmetic was eliminated based on the following argumentation: if we want to move from one random color to another, then it is sufficient to move the color in a certain time, in the direction of a random color vector. So instead of having a table with a list of random colors, and a program that changes the on-off duty cycles of the LEDs in such a way that the color of the LED follows the colors specified in the table, it is sufficient to have a table with only a list of random color directions or vectors. A nice idea, but is still needed multi-byte addition and subtraction. What was worse, it now becomes very difficult to have an absolute control over the colors that are produced in the sequence. I was afraid that the final color would continuously move in and around the boring white centre of the color triangle.
The final idea implemented here is more simple and transparent. The principle is based on a fast multiplexing with variable duty-cycle between two well defined colors COLA and COLB. By slowly varying the duty-cycle the color changes from COLA to COLB.
| to top of page | back to homepage |
The three color LEDs contain three LEDs in the primary colors: red, green and blue. As known, by varying the intensity of these three LEDs virtually any color can be synthesized [2,3,4].
The "old fashioned" analog way to do this is to adjust the current through the LED to obtain the desired intensity. This is however not very efficient and elegant. When an LED is biased somewhere in between fully off and fully on, a considerable amount of power will be dissipated by the driver circuit. Additionally, interfacing an analog driven LED to a digital processor requires quite a lot of circuitry such as DA converters and amplifiers.
A more modern and efficient driving scheme is pulse width modulation.
Using pulse width modulation, the LEDs are either switched fully on or fully
off with a simple switching transistor. In this way the amount of power
dissipated in the driver electronics is minimal.
When the LEDs is switched on and off at a sufficiently high frequency
so that the eye can not follow this pace (> 50Hz), the apparent
intensity of the LEDS will be proportional to the on/off duty cycle.
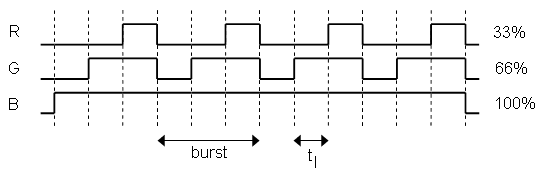
Figure 4. Example of the pulse width modulation used to drive the LEDs in this project. Each LED can be driven at four different intensity levels: 0%, 33%, 66% and 100%.
In this project a pulse width modulation scheme according to Fig. 4 is used.
In this example the composite color is a mixture of 100% blue, 66% green
and 33% red. Just to give the beast a name, I refer to the repetitive cycle
in Fig. 4 with "a burst". A burst has to have a length shorter than 20 ms
for the eye not to follow the switching of the LEDs. In this project four
levels of intensity for every color is used: 100%, 66%, 33% and off. These
four levels are coded with two bits, so that one byte is sufficient to
represent one composite color. In total 4*4*4=64 colors (including all LEDs
off) are possible. These colors are called the palette colors.
In reality a much larger off colors will be displayed
since one color fades slowly into another, resulting a random mixtures
of the 64 colors palette.
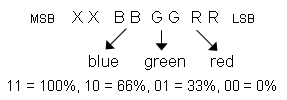
Figure 5. Each of the palette colors is represented by one byte. Two bits are used to specify the intensity of each of the three primary colors.
Fig. 5 shows how a byte representing a color is coded. The routine that
generates a burst is called every tl seconds. In this project
tl = 100 µs. Level counter `LCNT' is used to count through the four levels.
To make the program very fast and compact some tricks have been used.
Counter `LCNT' is initialized to value 3Fh. After every call (very next level),
it is decremented by 15h until the counter reaches zero. The subsequent values
of `LCNT' are thus 00111111B, 00101010B, 00010101B and 00000000B. The flow
diagram for the burst generator code is given in Fig. 6. At the beginning
of the routine `LCNT' is "XORed" with the specific color code. When the intensity
of one of the three colors equals the corresponding two bits in `LCNT', these
two bits will return 00, and the corresponding LED is switched on for the
remainder of the burst.
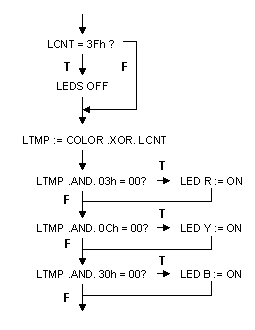
Figure 6. Flow diagram for the part of the program that generates a color burst.
| to top of page | back to homepage |
The previous section explained how a single color from the palette is generated.
In order to let one color `COLA', slowly fade into another color `COLB',
some kind of mixing of the two palette colors is needed.
This is done by fast multiplexing between the two colors `COLA' and `COLB'.
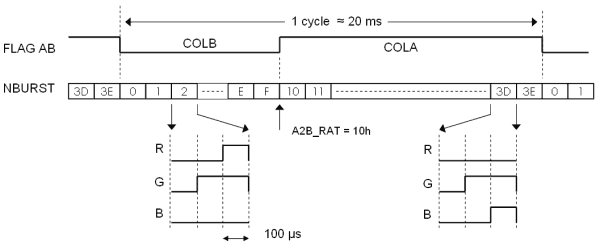
Figure 7. In a cycle two palette colors are mixed by multiplexing them with a variable duty-cyle.
Figure 7 shows how the mixing of colors `COLA' and `COLB' is implemented. During what is called a cycle `COLA' and `COLB' are displayed alternatingly. Each cycle consists of 63 bursts. Some burst display `COLA', others `COLB'. The variable `A2B_RAT' determines the mixing ratio between the two colors. When A2B_RAT=0 only `COLA' is displayed. When A2B_RAT=3Fh (64 decimal) only `COLB' is displayed. Flag `AB' determines which of the two colors is displayed and it is set when the burst counter `NBURST' equals `A2B_RAT'.
Initially I was afraid that all the manipulations involved were too time consuming to let the processor run on it's own internal 4 MHz clock. As it turned out I was mistaken as can be seen at the end of this page. However, I started out with using a 20 MHz external X-tal. In that case the internal clock frequency is 5 MHz (Fosc/4) corresponding to a period of 200 ns. With the prescaler of timer0 set at divide by 2, timer0 is incremented every 400 ns. As a result a roll-over from FFH to 00h (256 to 0) occurs every 256*0.4 µs= 102.4 µs. So the duration of one level is approximately 100 µs. The total length of a cycle is thus: 63*3*102.4 µ s=18.9 ms. This is short enough for eye to perceive it as one color without flickering.
| to top of page | back to homepage |
A complete color transition from `COLA' to `COLB' is reached when variable `A2B_RAT' is stepped from 00 to 40h. Each step is called a "transition step". The length of a transition step obviously determines the duration of a complete transition. The length of a transition step is determined by the number of (identical) cycles in the transition step and of course the duration of a cycle (102.4 µs). The number of cycles in a step is set in constant `NCYCLE_REL'. With only one cycle per transition step (NCYCLE_REL=1) a complete transition takes 64*18.9 ms= 1.21 s so approximately one second. By increasing `NCYCLE_REL' the transition time is increased proportionally.
| to top of page | back to homepage |
The sequence of colors that is displayed is stored in table `c_table'.
Each byte in this table represents one of the 64 palette colors (63 plus
LEDs off) coded according to Fig. 5. The last color in the table is followed
by FFh to indicate the end of the table.
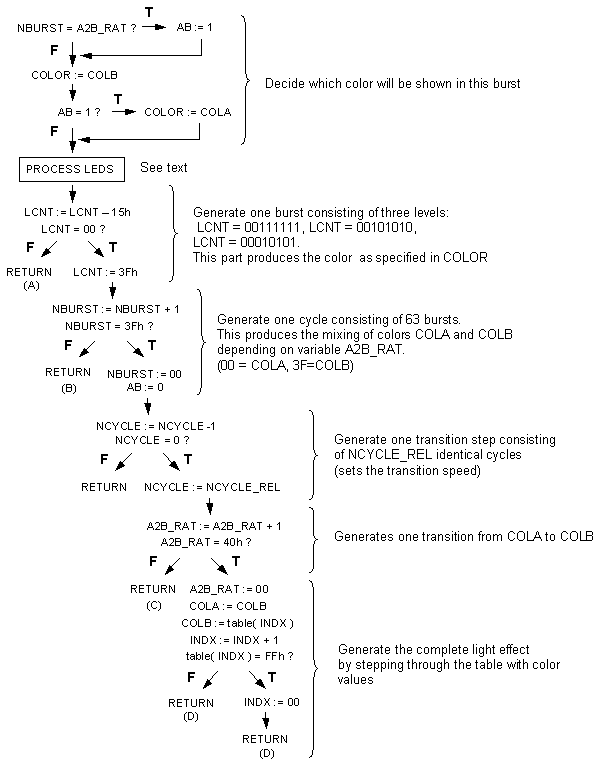
Figure 8. Complete flow diagram for the `rnd_col' routine. The box contains the color burst generating program of Fig. 6.
Stepping through the table is performed by a simple piece of code that advances table pointer `INDX' after every completed transition. Fig. 8 gives the complete flow diagram for the `rnd_col' routine
| to top of page | back to homepage |
As mentioned in one of the previous sections, the coding scheme with two bits per color allows for 4*4*4-1=63 palette colors. On inspection it was found that nine colors only consist of primary colors (Group 1), 27 colors use two primary colors (Group 2), whereas the remaining 27 colors are a combination of all three primary colors (Group 3).
I myself am partially color blind, so I am not a good judge of colors. Nevertheless, when playing with the different colors it appeared to me that all colors from the last group appeared a bit "whitish". I was affraid that too many of these "whitish" colors would make the light effects a bit boring, especially since during a transition two colors are again mixed, shifting the balance even more to the white. To compensate for this I made three different color tables with colors selected from the three groups.
Table 1 (group1.inc) only contains primary colors from group 1 in different intensities and in random order. During a transition obviously colors consisting of two primary colors are produced.
Table 2 (group2.inc) additionally contains colors consisting of two primary colors.
Table 3 (group3.inc) finally contains all possible palette colors. In order to pull the average of all the colors away from the "white centre" however, the colors from group 1 and group 2 have been over represented in ratio: group1 : group2 : group3 = 4:2:1. All three tables were generated by blind drawing of pieces of paper with a color on it.
In a "panel test", most people favored the colors from table 2. Somebody remarked that the colors produced by table 1 had a (too) high "lolly-pop" level. Most people found the colors from table 3 to much drawn to the white. As for myself, is is all pretty much the same to me!
| to top of page | back to homepage |
The program as it can be found in the download section at the end of this page is intended to run as a stand-alone application according in a 12F675A PIC processor according to the circuit diagram depicted in Fig. 1.
The program basically consists of three parts: 1. initialization of timer0, interrupts and variables, 2. the main program (empty in this case!), and 3. the interrupt service routine `rnd_col' which generates the color effects.
It is perfectly possible to combine routine `rnd_col' with other applications. The only requirement is that `rnd_col' is called every 100 µs. Here are some points of concern when `rnd_col' is used in another application:
| to top of page | back to homepage |
The amount of CPU time `rnd_col' uses varies. It is most when a transition is
complete, and a new color is loaded from the table. By simply counting
the instructions it was determined that `rnd_col' uses a maximum of 82
machine clock cycles. At a X-tal frequency of 20 MHz this amounts to
82*0.2 µs = 16.4 µs.
However, most of the calls to the routine will use much less CPU time.
To get a feeling for the average amount of CPU time used, a simple experiment
was performed. The normal IO instructions were replaced by NOP instructions,
and GPIO0 was made high at the beginning of 'rnd_col', and low again just
before the return instruction. In this way GPIO0 is high when the CPU is
actually executing instructions from 'rnd_col' and low when it runs the
main program and waits for the next interrupt.
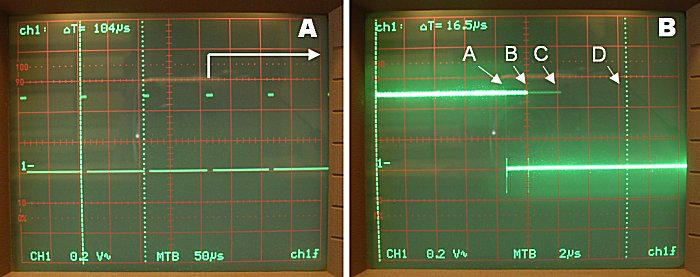
Figure 9s. Experiment to asses the amount of CPU time used by `rnd_col' for X-tal=20 MHz. The Labels A,B,C and D correspond to the labels on the returns in Fig. 8.
Figure 9 shows the scope trace of GPIO0. Figure 9A confirms that the routine is called about every 104 µs. It also shows that 'rnd_col' consumes relatively very little CPU time. Figure 9B again depicts the signal at GPIO0, but now at 2 µs/div. The scope always triggers on the rising edge of the signal so that the different negative edges correspond to the different returns in the routine. The brighter the trace, the more often this part of the routine is executed. The different returns have been marked with labels which correspond to the labels in Fig. 8. From Fig. 9B it seems fair to estimate that the routine on average takes about 10 µs of CPU time.
An alternative, and more precise way to measure the average CPU usage, would have been to connect an (analog) volt meter to GPIO0. The average percentage of CPU usage would then be given by (V/5)*100%.
| to top of page | back to homepage |
From the calculations and measurements in the previous section it became clear that the 'rnd_col' at maximum consumes about 16.5 us at a clock frequency of 20 MHz. This implies that when a clock frequency of 4 MHz is used, the maximum CPU usage would amount to 16.5*(20/4)= 82.5 us. Since this is still less than the interrupt rate of 100 us, it would still work! This is great because now the internal 4 MHz oscillator can be used without the need for any external timing components.
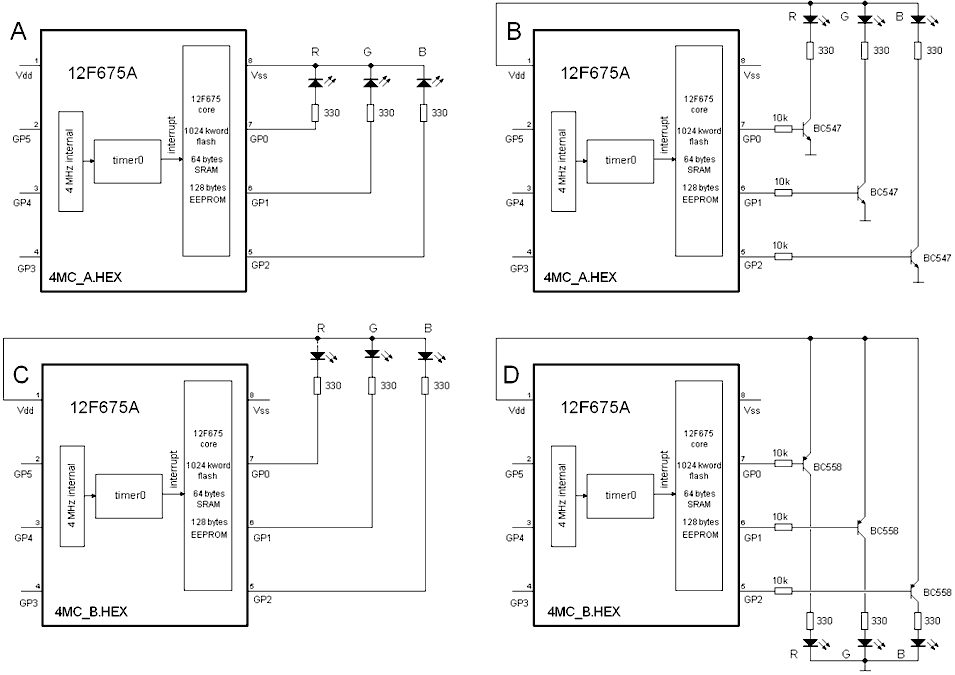
Figure 10. Circuit diagram of the 4 MHz version of the random color circuit. There are 4 versions for common anode or common cathode LEDs, with and without external transistors. Note that the 5 Volt power connection to Vdd and the ground connection to Vss have not been drawn.
Figure 10 depicts four variants of the 4 MHz version of the circuit. The top two versions (Fig. 10 A and B) have active high outputs meaning that the when the output is high the LED is on. In Fig. 10A the outputs directly drive a common cathode LED. Note that in this case the current per LED has to be limited to ca. 20 mA. In Fig. 10B the LED(s) are driven by an external transistor. In this case more LED(s) can be driven. Both versions use the same program version: 4MC_A.HEX. The bottom two versions (Fig. 10 C and D) have active low outputs meaning that the when the output is low the LED is on. In Fig. 10C the outputs directly drive a common anode LED. In Fig. 10D the LED(s) are driven by an external pnp transistor. In this case a common cathode LED is used. Both version C and D use the same program version: 4MC_D.HEX. Apart from the components shown no other components are necessary. Not shown in the figure are the power supply connections: ground to Vss and +5 V to Vdd. The components are not critical as long as the maximum output current of the PIC is limited to 20 mA per IO. For the transistors any general purpose npn or pnp type can be used.
With respect to the 20 MHz version a few small modifications in the program were required. In the first place the configuration word was modified so that the processor runs on the internal osillator instead of the external X-tal oscillator. Secondly, in the
20 MHz version, the 100 us interrupt is generated by a roll-over from
Timer0. Quite accidentally it turned out that no Timer0 reload was necessary in that case. For the 4 MHz version however, only 256*(4/20) ≈ 50 counts of Timer0 are needed for an interrupt every 100 us. Theoretically this would mean that Timer0 has to be reloaded to 256-50=206=CEh after every interrupt. Playing with the circuit is was found that a reload value of B8h gave a slightly better result. Finally for the “active low” version obviously some instructions had to be modified.
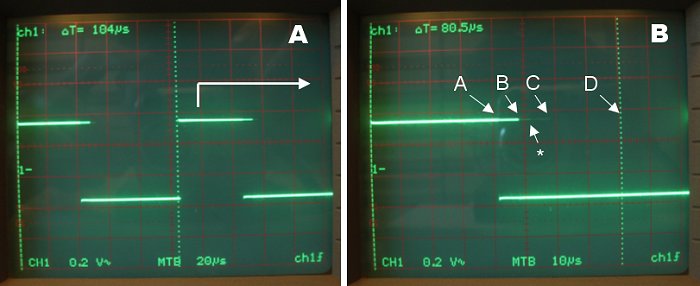
Figure 11. Experiment to assess the amount of CPU time used by `rnd_col' when using the internal 4 MHz oscillator. The Labels A,B,C and D correspond to the labels on the returns in Fig. 8.
Figure 11 depicts the CPU usage for the 4 MHz version. Although the average CPU usage is still less than 50%, the maximum CPU usage can be as high as 80%, leaving only 20% for the main program. This may make it difficult to run 'rnd_col'on the back-ground of another application.

Figure 12. Front and backside of Jan's clock with yours truly, who is very grateful for the invention of double sided adhesive tape!
| to top of page | back to homepage |
The zip file that you can download here contains the following files:

Theo Michielsen Joint Philips Research in 1967 at the age of 14. In 2007 he celebrated his 40th year jubilee working with the Research Lab. Trained as a glass craftsman and lens maker he spend the last twenty years on grinding, lapping, polishing a enormous variety materials. One of his standard methods to inspect polished substrates is to use oblique lighting (scheerlicht). The little glass man represents Theo inspecting a substrate. It was made by Jan Leyten and it was probably one of the last “products” of the glass-blowing workshop.


Eduard Meijer spent a large part of his working career at Philips Research on Color Detection and color control of LEDs. In 2011 Eduard left Philips to pursue a career as a medical physics at the Maxima Medical Centre. It was therefore very appropriate that we made him a present in which LEDs and Colors feature prominently. In this case an array of color changing LEDs is positioned behind a glass wafer containing sub-micron aluminum patterns, which cause a color dependent diffraction of the light. A nice present for a nice guy who is still missed daily.


From 2006-2012 Derk Reefman was the department head of the group “Micro-system and Devices” at Philips Research. He did such a good job that we were all very sorry that he left. Obviously we also wanted to make a present for him, but unfortunately, as a result of continuing rationalization processes and shrinking budgets, the good old custom of “homemade” farewell presents has become “almost” impossible. So instead of making him a present, we thought it would be nice to make something that we could put on the wall in one of the offices and that would remind us of him. However, when it was finished nobody would have it in his office, so in the end, just to get rid of it, we decided to give it to him.